Fractal Elasticity along the straight line curve.
Fractal Elasticity - along the straight line curve.
Click to see the most recent developments that complement this entry.
After discovering in my early blog that the elasticity of the Koch Snowflake fractal is constant, I have since pondered what the meaning of all this is.
Economic theory suggests that all objects have constant elasticity or are logarithmic in nature. The next step is to straighten out the fractal curves.
I produced the following diagrams to do just that and to demonstrate the change in fractal elasticity as the fractal developments. The above diagram shows constant elasticity and the below variable elasticity along the straight (log) curve.
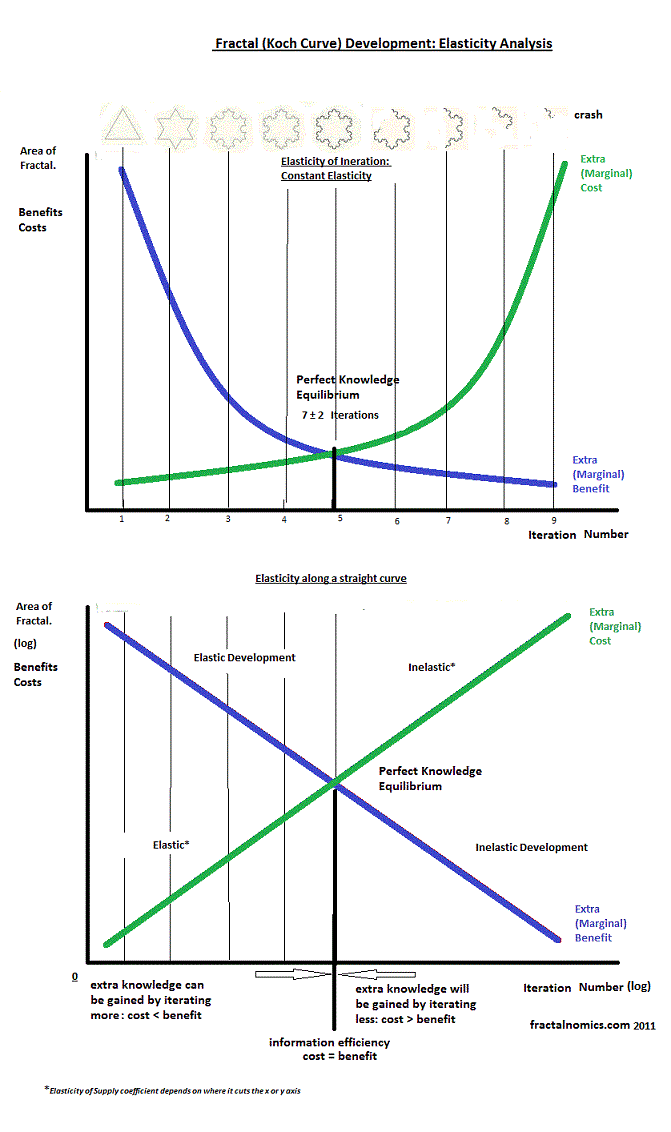
What is the significance of elasticity?
Elasticity along a straight-line curve will vary along its length from highly elastic (elastic) to low elasticity (inelastic).
What does it mean? Highly elastic—at the early stages of development—suggests another iteration or experience will provide high benefit, utility, or satisfaction—it is exciting, it is new. Conversely, inelastic—at later stages of development—suggests another iteration or experience will provide little added benefit, from euphoria (in the beginning) to boredom ( in the end).
Cost Elasticity
What I take from this is that we are insensitive to cost in the early stages of development. As we develop, we become more cost-sensitive. More on this later.
As I have stated on the diagram, marginal cost elasticity depends on where the line cuts the x or y-axis. However, I have found that the coefficient always starts high (or elastic) and runs to low, so I am confident in my above statement.
For more, take a look at these diagrams (2012).
Update May 2017
This is by far my best idea; I have written it up in a working paper at my academia.edu and vixra, and named it: Quantum Mechanics, Information and Knowledge, all Aspects of Fractal Geometry and Revealed in an Understanding of Marginal Economics.
I shall post the abstract, followed by the original post, and then the paper. I hope to have some collaborate and review my work in time.
Click to see the most recent developments that complement this entry.
After discovering in my early blog that the elasticity of the Koch Snowflake fractal is constant, I have since pondered what the meaning of all this is.
Economic theory suggests that all objects have constant elasticity or are logarithmic in nature. The next step is to straighten out the fractal curves.
I produced the following diagrams to do just that and to demonstrate the change in fractal elasticity as the fractal developments. The above diagram shows constant elasticity and the below variable elasticity along the straight (log) curve.

What is the significance of elasticity?
Elasticity along a straight-line curve will vary along its length from highly elastic (elastic) to low elasticity (inelastic).
What does it mean? Highly elastic—at the early stages of development—suggests another iteration or experience will provide high benefit, utility, or satisfaction—it is exciting, it is new. Conversely, inelastic—at later stages of development—suggests another iteration or experience will provide little added benefit, from euphoria (in the beginning) to boredom ( in the end).
Cost Elasticity
What I take from this is that we are insensitive to cost in the early stages of development. As we develop, we become more cost-sensitive. More on this later.
As I have stated on the diagram, marginal cost elasticity depends on where the line cuts the x or y-axis. However, I have found that the coefficient always starts high (or elastic) and runs to low, so I am confident in my above statement.
For more, take a look at these diagrams (2012).
Update May 2017
This is by far my best idea; I have written it up in a working paper at my academia.edu and vixra, and named it: Quantum Mechanics, Information and Knowledge, all Aspects of Fractal Geometry and Revealed in an Understanding of Marginal Economics.
I shall post the abstract, followed by the original post, and then the paper. I hope to have some collaborate and review my work in time.
Abstract
Fractal geometry is found universally and is said to be one of the best descriptions of our reality – from clouds and trees to market price behaviour. As a fractal structure emerges – the repeating of a simple rule – it appears to share direct properties familiar to classical economics, including production, consumption, and equilibrium. This paper investigated whether the mathematical principles behind ‘the market’ – known as marginalism – is an aspect or manifestation of a fractal geometry or attractor. Total and marginal areas (assumed to stand for utility) and the cost of production were graphed as the fractal grew and compared to a classical interpretation of diminishing marginal utility theory and the market supply and demand. PED and PES were also calculated and analysed with respect to (iteration) time and decay. It was found that the fractal attractor demonstrates properties and best models classical economic theory, and from this, it was deduced that the market is a fractal attractor phenomenon where all properties are inextricably linked. The fractal, at equilibrium, appears to be a convergent – zeta function – series, able to be described by Fourier analysis and involves Pi, i, e, 0, and 1 (of Euler’s identity) in one model. It also demonstrated growth, development, evolution and Say’s Law – production before consumption. Insights from the fractal on knowledge and knowing are also revealed, with implications on the question of what exactly is ‘science’ – and what is ‘art’? A connection between reality and quantum mechanics was identified. It was concluded marginal classical economics is an aspect of fractal geometry.
Keywords
Marginal, Fractal, Elasticity, Utility, Cost, Production, Price, Growth and Development, Say’s Law



So we could say the degree of elasticity is also known as the measure of value?
ReplyDelete