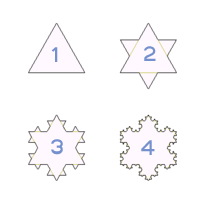
1.8 Sustainability and the Fractal

Sustainability and the fractal: This entry follows on from my fractal growth and development entries, which were published earlier. There is never one snowflake alike, but there are snowflakes. The fractal offers insights and helps us understand growth and development, change and evolution. It should also help us understand sustainability . It should clarify what sustainability is. Is it real? Is it possible? Is it an illusion, or is it a delusion? Fractals, by definition, are patterns that show: 'same' but 'different' or regular irregularity - at all scales. Fractals support sustainability in one way but not in another or the way we currently associate sustainability with keeping the environment or the economy today without compromising future generations. It may be that the notion of sustainability is (mathematically) nonsense. Here's why. Fractals and sustainability analysis To see why sustainability is a false statement and doesn't h...