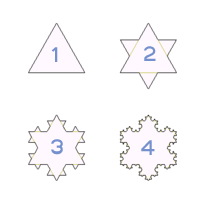
Fractal: Growth and Development
Update 2010-12-05 Growth and Development Take a long look at the fractals above and ask yourself: are they developing? Are they growing? There appears (to me) to be no obvious or distinguishing differences between (fractal) growth and (fractal) development. When describing fractals, the terms growth and or development are often used interchangeably. As if to be a law, the fractal fact is that the two are inextricably linked - as the fractal grows, the fractal develops. development The fractal demonstrates Development: this has to do with the increase in complexity of a fractal as it iterates towards fractal equilibrium; it is a qualitative measure of fullness and completeness. growth The fractal (also) demonstrates Growth and may be seen as an increase in either the area, number of triangles, or even the perimeter of the snowflake - which is apparently infinite. To analyse growth (more), we must look back at one of the early diagrams I 'developed' (above).