(Christmas) tree Lorenz Curve
After completing my Lorenz analysis of the Koch Snowflake fractal, I set about analysing a real-life fractal and chose a Christmas tree. This has been a side interest from my core fractal work and thinking, so I have not written it up as a 'science report'.
I don't know which species of tree I selected, but it is a typical conifer of the northern hemisphere.
Method
I trimmed all the branches off the tree, counted them, weighed them, recorded results, then ranked the branches from lightest to heaviest, completed a cumulative percentage rank of weight and count table, and finally graphed the results.
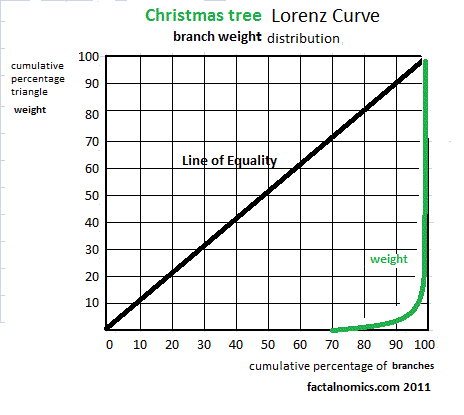
Below is the Christmas tree Lorenz Curve in terms of weight. Note that 'cumulative percentage of triangle weight' should read branch rather than a triangle.
I found that there were 5 levels of branches.
I will be honest with you. I did not continue counting and weighing the branches in detail after the third level—the time cost was just too high, and it would not change their shape as they were so light. So, I counted and averaged the final two levels (sorry, things to do).
I don't know which species of tree I selected, but it is a typical conifer of the northern hemisphere.
Method
I trimmed all the branches off the tree, counted them, weighed them, recorded results, then ranked the branches from lightest to heaviest, completed a cumulative percentage rank of weight and count table, and finally graphed the results.
 |
| Branches everywhere: |
I found that there were 5 levels of branches.
I will be honest with you. I did not continue counting and weighing the branches in detail after the third level—the time cost was just too high, and it would not change their shape as they were so light. So, I counted and averaged the final two levels (sorry, things to do).
Conclusion and reflection
The conifer tree has a very large Gini coefficient - similar to the Koch snowflake (below) and the standard wealth distribution.
The question is, is this how an economy is? Is this distribution universal? Yes, it is.
Is improving this Gini coefficient impossible? Do we see Chrismas trees with branches as big a the trunk? No - the branches will break.
This makes me think of cacti, but the trunk is dominant.
That was fun. I would like to thank my family, who promised not to laugh while I counted branches on the floor :), my school math teacher colleagues for their support, and, of course—always—my students.
Update 2017, I have published/posted.
I have found that Lorenz distribution is a fractal phenomenon. The fractal models the Lorenz Curve. Gini coefficients increase as the fractal grows and develops, and the distribution between groups accelerates with growth and development. Lorenz distribution is universal, with income and wealth inequality being one aspect of it. It is also scale invariant.
https://www.academia.edu Demonstrating_Lorenz_Wealth_Distribution_and_Increasing_Gini_Coefficient_with_the_Iterating_Koch_Snowflake_Fractal_Attractor
I have found that Lorenz distribution is a fractal phenomenon. The fractal models the Lorenz Curve. Gini coefficients increase as the fractal grows and develops, and the distribution between groups accelerates with growth and development. Lorenz distribution is universal, with income and wealth inequality being one aspect of it. It is also scale invariant.
https://www.academia.edu Demonstrating_Lorenz_Wealth_Distribution_and_Increasing_Gini_Coefficient_with_the_Iterating_Koch_Snowflake_Fractal_Attractor





"The question is, is this how an economy is? Is this disribution universal? Yes it is.
ReplyDeleteIs improving this gini coefficient impossible? Do we see Chrismas trees with branches as big a the trunk? No - the branches will break."
But the difference is that an economy is far different from a tree. It's a political choice. People are not branches of a single organism. People are organisms ourselves. It is definitely possible to lower the Gini of an economy. Imagine if the USA taxed wealth instead of wages. That would help. Please, you cannot use some metaphor from a spruce to an economy and then accept the crushing inequality that kills people.
Third, get the correct sort of Christmas Candle for your light holders. The fit is essential, so it's not worth compromising or endeavoring to substitute another sort of flame. The light truly must be cozy in the base of the holder for wellbeing reasons. Birthday candles are too thin.http://paramatan.com/best-christmas-tree-stands/
ReplyDeleteYou ought to likewise take a gander at the leaves. Little leaves, near one another, help make an ample hallucination when in actuality the branch is so little, there is constrained space for bounty. go
ReplyDelete